Introduction to Data Mining (Datawhale)

Very basic introduction to data mining.

Introduction

Exploratory-Data-Analysis

Exploratory Data Analysis

What is EDA

EDA is like detective work: Exploratory data analysis is an attitude, a state of flexibility, a willingness to look for those things that we believe are not there, as well as those that we believe to be there.

EDA is active and incisive: Exploratory data analysis is actively incisive rather than passively descriptive, with real emphasis on the discovery of the unexpected.

Philosophy of EDA

• Confirm understanding of the data
• Keep an open mind and be willing to find something surprising
• Iterate procedures below
  • Uncover new aspects of our data
  • Re-examine our understanding of the data
  • Continue exploration

To Carry Out EDA

Connect what you find to the question and context

• Plot data in multiple ways to get different insights
• Transform variables to symmetrize distributions
• Transform to straighten relationships
• Derive new variables
• Consider effect of other variables on distributions &
  elationships

Something about Basic Data Visualize

Features Seen in a Visual Summary

• Mode(s) - values concentrate around particular points
• Symmetry – skew left, symmetric, skew right distribution of values about center
• Tails - long, short, normal (what expect for normal distribution)
• Gaps - regions where no values observed
• Outliers - unusually large/small values

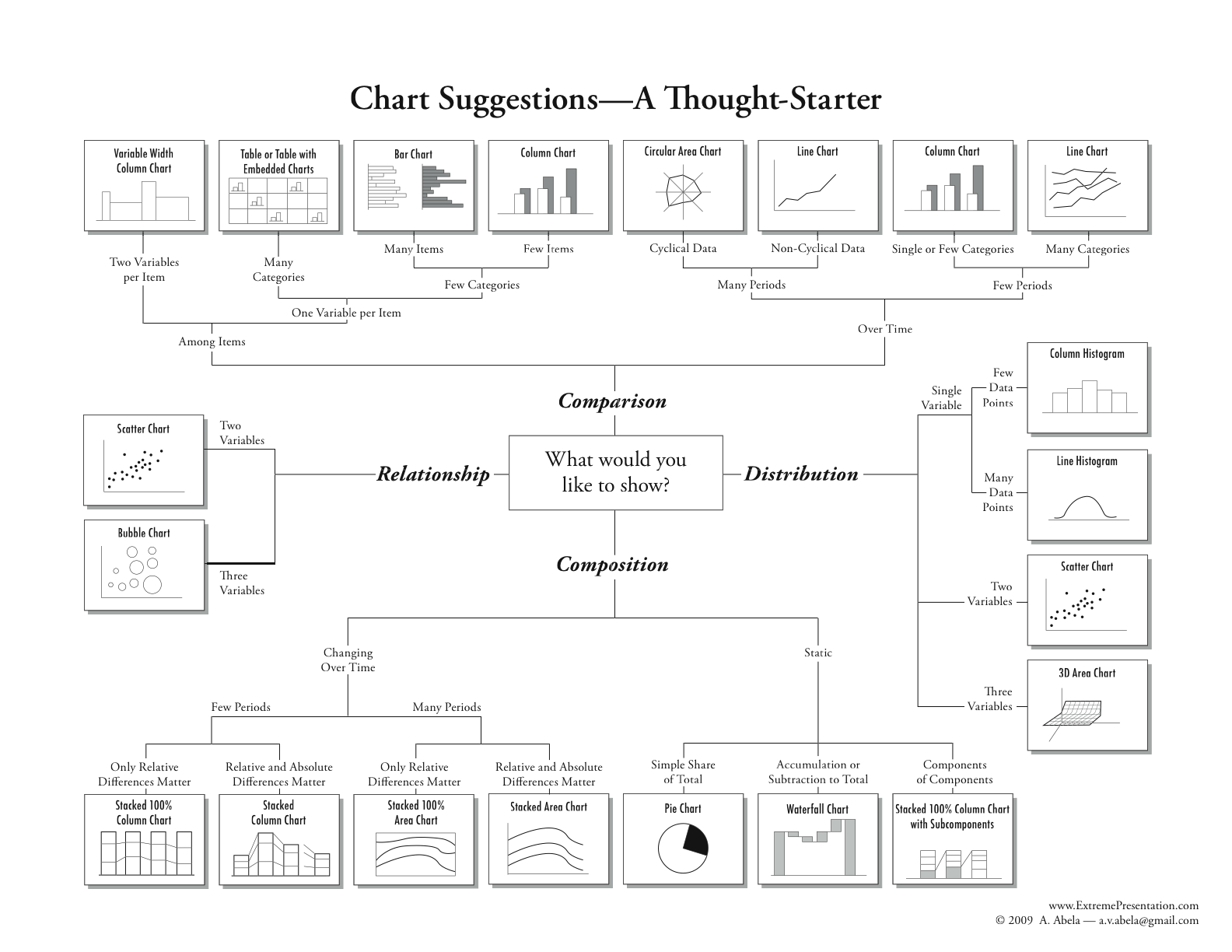
Choose Proper Charts

Practice

import os
import shutil
import numpy as np
import pandas as pd
import pandas_profiling as pdpf
import time

import warnings
warnings.filterwarnings('ignore')

import matplotlib
import matplotlib.pyplot as plt
import seaborn as sbn
%matplotlib inline

import missingno as msno
import pivottablejs

import lightgbm as lgb
import xgboost as xgb

from sklearn.decomposition import PCA, FastICA, FactorAnalysis, SparsePCA

from sklearn.model_selection import GridSearchCV, cross_val_score, StratifiedKFold, train_test_split
from sklearn.metrics import mean_squared_error, mean_absolute_error

os.chdir(r"D:\Tianchi")

def Sta_inf(data):
    print('-'*20 + 'Statistic Info' + '-'*20 +'\n')
    print('_min =\n',np.min(data))
    print('_max =\n',np.max(data))
    print('_mean =\n',np.mean(data))
    print('_ptp =\n',np.ptp(data))
    print('_std =\n',np.std(data))
    print('_var =\n',np.var(data))

''' 数据含义
SaleID 	交易ID，唯一编码
name 	汽车交易名称，已脱敏
regDate 	汽车注册日期，例如20160101，2016年01月01日
model 	车型编码，已脱敏
brand 	汽车品牌，已脱敏
bodyType 	车身类型：豪华轿车：0，微型车：1，厢型车：2，大巴车：3，敞篷车：4，双门汽车：5，商务车：6，搅拌车：7
fuelType 	燃油类型：汽油：0，柴油：1，液化石油气：2，天然气：3，混合动力：4，其他：5，电动：6
gearbox 	变速箱：手动：0，自动：1
power 	发动机功率：范围 [ 0, 600 ]
kilometer 	汽车已行驶公里，单位万km
notRepairedDamage 	汽车有尚未修复的损坏：是：0，否：1
regionCode 	地区编码，已脱敏
seller 	销售方：个体：0，非个体：1
offerType 	报价类型：提供：0，请求：1
creatDate 	汽车上线时间，即开始售卖时间
price 	二手车交易价格（预测目标）
v系列特征 	匿名特征，包含v0-14在内15个匿名特征
'''

data_train = pd.read_csv(r'data/used_car_train_20200313.csv', encoding='utf-8', sep=' ', )
data_test = pd.read_csv(r'data/used_car_testA_20200313.csv', encoding='utf-8', sep=' ', )
data_train.info()
print('-'*20)
print(data_train.head())
print('-'*20)
print(data_train.describe().iloc[:,0:4])

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 150000 entries, 0 to 149999
Data columns (total 31 columns):
SaleID               150000 non-null int64
name                 150000 non-null int64
regDate              150000 non-null int64
model                149999 non-null float64
brand                150000 non-null int64
bodyType             145494 non-null float64
fuelType             141320 non-null float64
gearbox              144019 non-null float64
power                150000 non-null int64
kilometer            150000 non-null float64
notRepairedDamage    150000 non-null object
regionCode           150000 non-null int64
seller               150000 non-null int64
offerType            150000 non-null int64
creatDate            150000 non-null int64
price                150000 non-null int64
v_0                  150000 non-null float64
v_1                  150000 non-null float64
v_2                  150000 non-null float64
v_3                  150000 non-null float64
v_4                  150000 non-null float64
v_5                  150000 non-null float64
v_6                  150000 non-null float64
v_7                  150000 non-null float64
v_8                  150000 non-null float64
v_9                  150000 non-null float64
v_10                 150000 non-null float64
v_11                 150000 non-null float64
v_12                 150000 non-null float64
v_13                 150000 non-null float64
v_14                 150000 non-null float64
dtypes: float64(20), int64(10), object(1)
memory usage: 35.5+ MB
--------------------
   SaleID    name   regDate  model  brand  bodyType  fuelType  gearbox  power  \
0       0     736  20040402   30.0      6       1.0       0.0      0.0     60   
1       1    2262  20030301   40.0      1       2.0       0.0      0.0      0   
2       2   14874  20040403  115.0     15       1.0       0.0      0.0    163   
3       3   71865  19960908  109.0     10       0.0       0.0      1.0    193   
4       4  111080  20120103  110.0      5       1.0       0.0      0.0     68   

   kilometer  ...       v_5       v_6       v_7       v_8       v_9      v_10  \
0       12.5  ...  0.235676  0.101988  0.129549  0.022816  0.097462 -2.881803   
1       15.0  ...  0.264777  0.121004  0.135731  0.026597  0.020582 -4.900482   
2       12.5  ...  0.251410  0.114912  0.165147  0.062173  0.027075 -4.846749   
3       15.0  ...  0.274293  0.110300  0.121964  0.033395  0.000000 -4.509599   
4        5.0  ...  0.228036  0.073205  0.091880  0.078819  0.121534 -1.896240   

       v_11      v_12      v_13      v_14  
0  2.804097 -2.420821  0.795292  0.914762  
1  2.096338 -1.030483 -1.722674  0.245522  
2  1.803559  1.565330 -0.832687 -0.229963  
3  1.285940 -0.501868 -2.438353 -0.478699  
4  0.910783  0.931110  2.834518  1.923482  

[5 rows x 31 columns]
--------------------
              SaleID           name       regDate          model
count  150000.000000  150000.000000  1.500000e+05  149999.000000
mean    74999.500000   68349.172873  2.003417e+07      47.129021
std     43301.414527   61103.875095  5.364988e+04      49.536040
min         0.000000       0.000000  1.991000e+07       0.000000
25%     37499.750000   11156.000000  1.999091e+07      10.000000
50%     74999.500000   51638.000000  2.003091e+07      30.000000
75%    112499.250000  118841.250000  2.007111e+07      66.000000
max    149999.000000  196812.000000  2.015121e+07     247.000000

col_num_train = data_train.select_dtypes(exclude='object').columns
print(col_num_train)
col_cat_train = data_train.select_dtypes(include='object').columns
print(col_cat_train)

col_num_test = data_test.select_dtypes(exclude='object').columns
col_cat_test = data_test.select_dtypes(include='object').columns

Index(['SaleID', 'name', 'regDate', 'model', 'brand', 'bodyType', 'fuelType',
       'gearbox', 'power', 'kilometer', 'regionCode', 'seller', 'offerType',
       'creatDate', 'price', 'v_0', 'v_1', 'v_2', 'v_3', 'v_4', 'v_5', 'v_6',
       'v_7', 'v_8', 'v_9', 'v_10', 'v_11', 'v_12', 'v_13', 'v_14'],
      dtype='object')
Index(['notRepairedDamage'], dtype='object')

featured_cols = [col for col in col_num_train if 'Type' not in col\
                 and col not in ['SaleID','name','regDate','creatDate','price','model','brand','regionCode','seller']]
data_train_X = data_train[featured_cols]
data_train_Y = data_train['price']
data_train_X.fillna(-1)
data_train_Y.fillna(-1)
data_test_X = data_test[featured_cols]
print('X train shape =',data_train_X.shape)
print('X test shape =',data_test_X.shape)

X train shape = (150000, 18)
X test shape = (50000, 18)

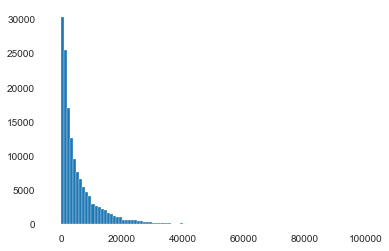
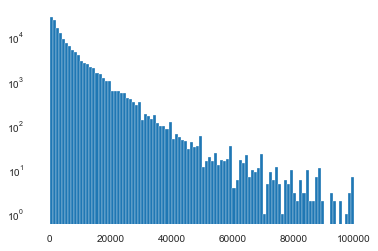
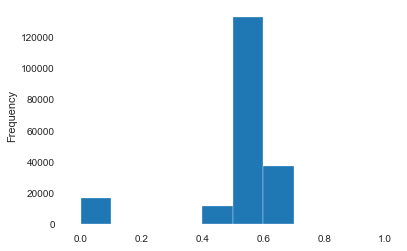
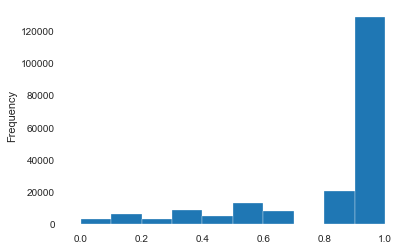
Sta_inf(data_train_Y)
plt.hist(data_train_Y,bins=100, log=False)
plt.show()
plt.hist(data_train_Y,bins=100, log=True)
plt.show()
plt.close()

--------------------Statistic Info--------------------

_min =
 11
_max =
 99999
_mean =
 5923.327333333334
_ptp =
 99988
_std =
 7501.973469876635
_var =
 56279605.942732885

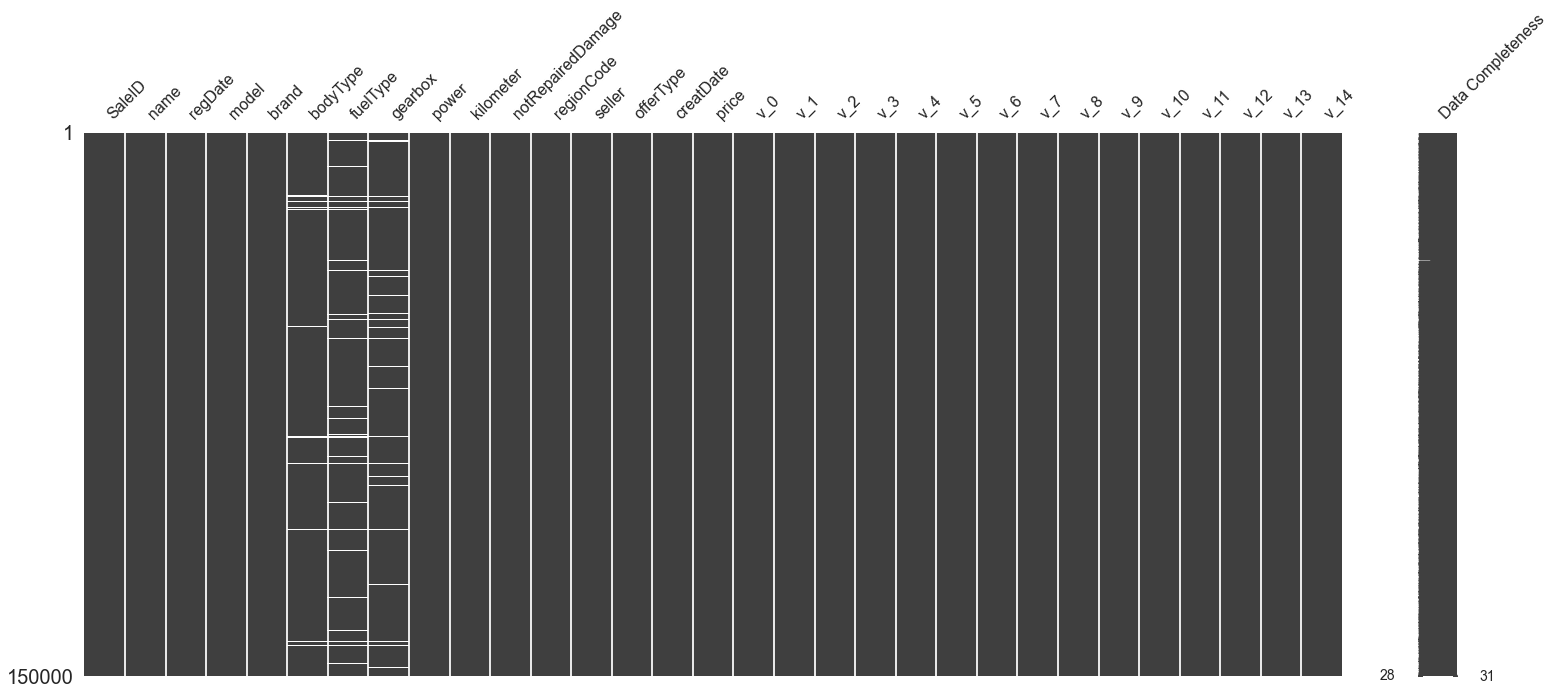
msno.matrix(data_train, labels=True)

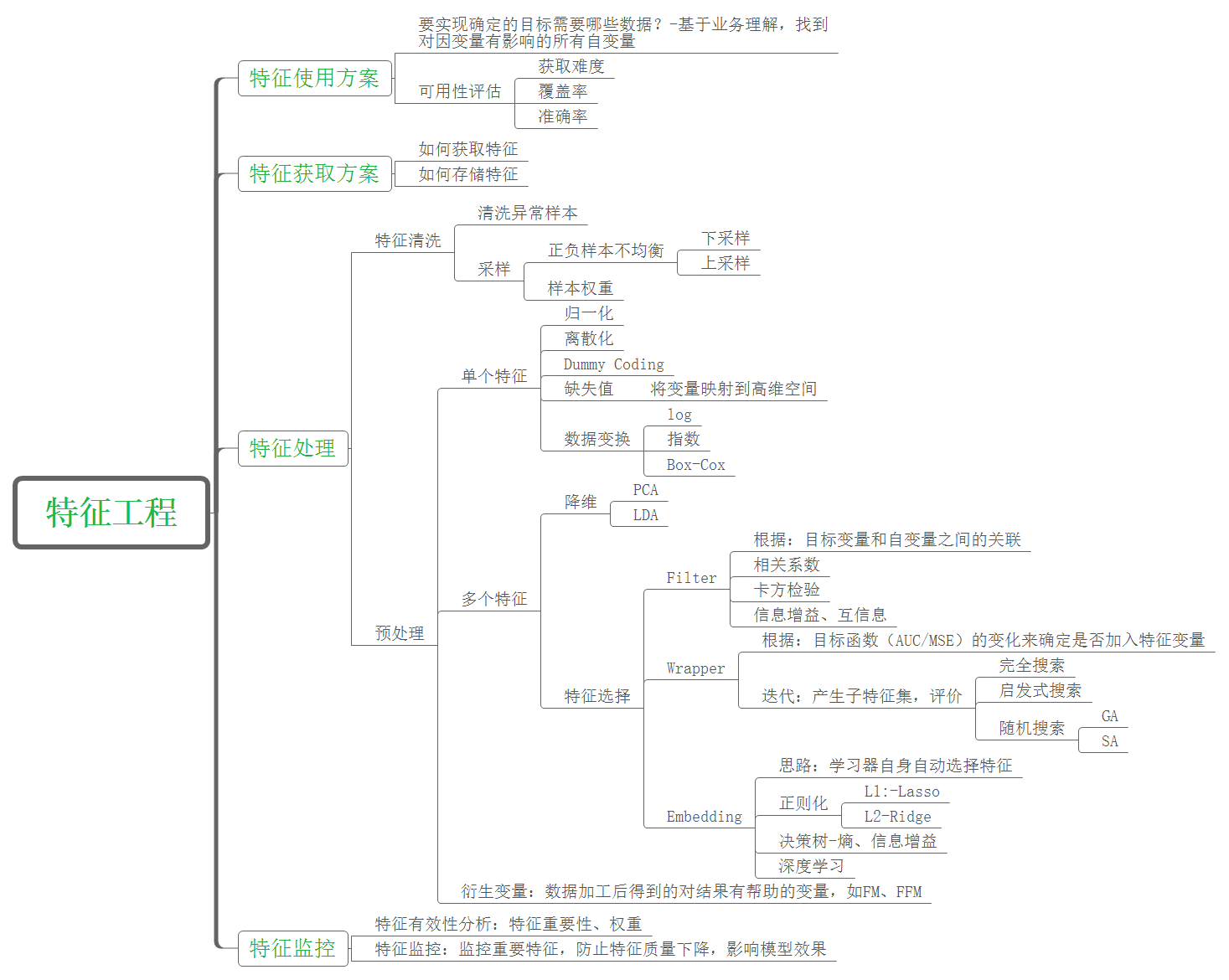
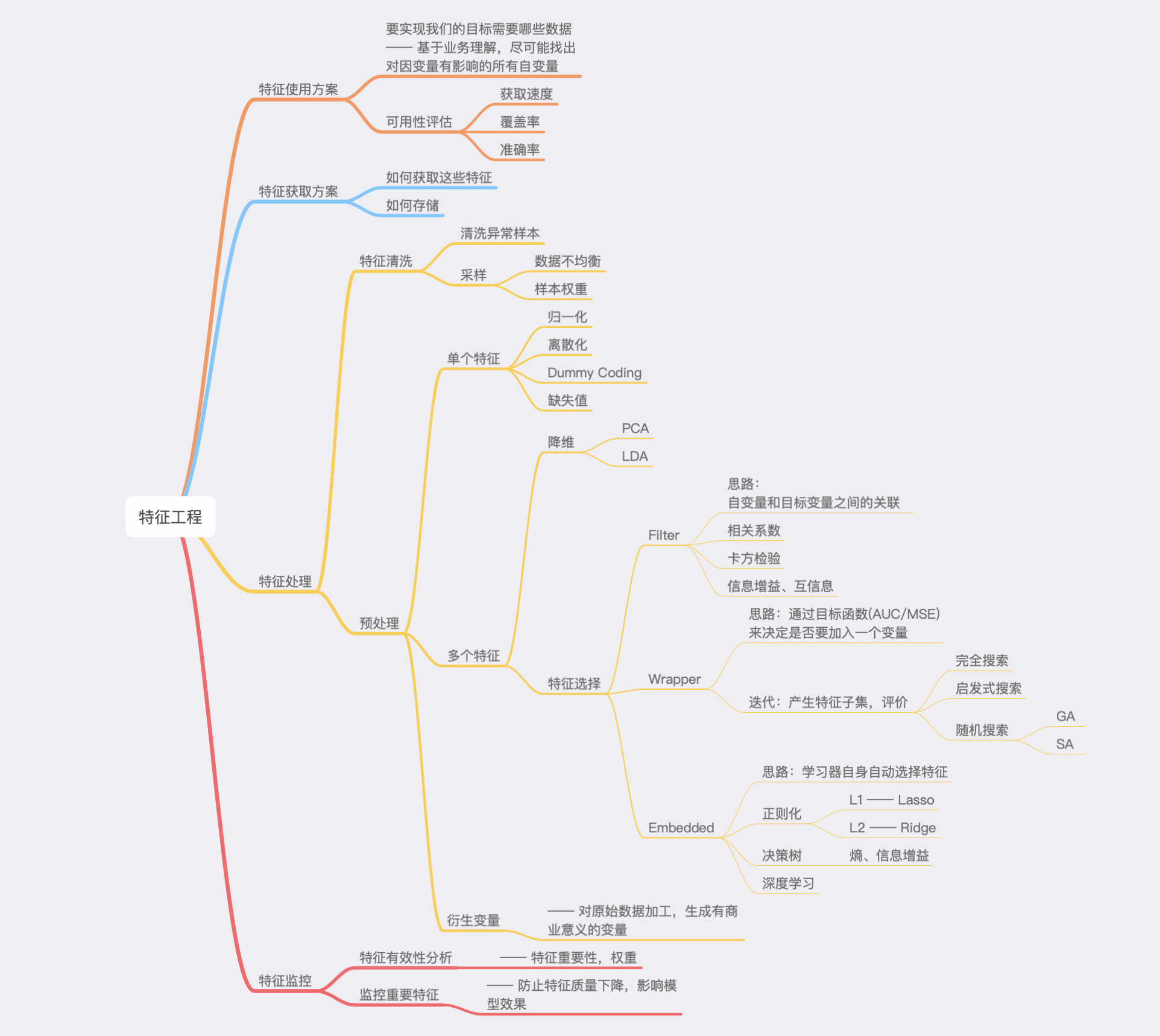
Feature Engineering

Feature Engineering

What is FE

特征工程的主要目的还是在于将数据转换为能更好地表示潜在问题的特征，从而提高机器学习的性能。比如，异常值处理是为了去除噪声，填补缺失值可以加入先验知识等。

特征构造也属于特征工程的一部分，其目的是为了增强数据的表达。

FE BASIC

有些数据的特征是匿名特征，这导致我们并不清楚特征相互直接的关联性，这时我们就只有单纯基于特征进行处理，比如装箱，groupby，agg 等这样一些操作进行一些特征统计，此外还可以对特征进行进一步的 log，exp 等变换，或者对多个特征进行四则运算、多项式组合等然后进行筛选。由于特性的匿名性其实限制了很多对于特征的处理，当然有些时候用 NN 去提取一些特征也会达到意想不到的良好效果。

对于知道特征含义的特征工程，特别是在工业类型比赛中，会基于信号处理，频域提取，丰度，偏度等构建更为有实际意义的特征，这就是结合背景的特征构建，在推荐系统中也是这样的，各种类型点击率统计，各时段统计，加用户属性的统计等等，这样一种特征构建往往要深入分析背后的业务逻辑或者说物理原理，从而才能更好的找到 magic。

当然特征工程其实是和模型结合在一起的，这就是为什么要为 LR NN 做分桶和特征归一化的原因，而对于特征的处理效果和特征重要性等往往要通过模型来验证。

To Carry Out FE

1. 特征预处理

   • 缺失值处理
     • 不处理（针对类似 XGBoost 等树模型）
     • 删除（缺失数据太多）
     • 插值补全，包括均值/中位数/众数/建模预测/多重插补/压缩感知补全/矩阵补全等
     • 分箱，缺失值一个箱
   • 归一化
     • 标准化（转换为标准正态分布）
     • 归一化（抓换到 [0,1] 区间）
     • 针对幂律分布，可以采用公式：$\log{\frac{1+x}{1+median}}$
   • 异常值与数值截断
     • 通过箱线图（或 3-Sigma）分析删除异常值
     • BOX-COX 转换（处理有偏分布）
     • 长尾截断
   • 非线性变换
   • 无量纲处理

2. 特征构建

   • 离散特征
     • one-hot编码
     • 散列编码
     • 计数编码
     • 离散特征之间交叉
     • 离散特征与连续特征交叉
   • 连续(数值)特征
     • 特征交叉
     • 离散化(分桶)
       • 等距
       • 等频
       • 模型
   • 时空特征
     • 转化为数值
     • 将时间离散化
     • 行政区划表示
     • 经纬度表示
     • 距离表示
   • 文本特征
     • TF-IDF、LDA / Word2Vec
   • 富媒体特征
   • 嵌入特征

3. 特征选择

   • 基于统计量选择 / Filter: 过滤法，按照发散性或者相关性对各个特征进行评分，设定阈值或者待选择阈值的个数，选择特征。
     • 选择方差大的特征: 分布均匀的特征，样本之间差别不大，该特征不能很好区分不同样本，而分布不均匀的特征，样本之间有极大的区分度，因此通常可以选择方差较大的特征，去掉方差变化小的特征。具体方差多大算大，可以事先计算出所有特征的方差，选择一定比例(比如20%)的方差大的特征，或者可以设定一个阈值，选择方差大于阈值的特征。
     • 皮尔逊相关系数: 用于衡量变量之间的线性相关性，取值区间为[-1，1]
     • 覆盖率: 特征的覆盖率是指训练样本中有多大比例的样本具备该特征。我们首先计算每个特征的覆盖率，覆盖率很小的特征对模型的预测效果作用不大，可以剔除。
     • 假设检验： 对于特征变量为类别变量而目标变量为连续数值变量的情况，可以使用方差分析，对于特征变量和目标变量都为连续数值变量的情况，可以使用皮尔森卡方检验。卡方统计量取值越大，特征相关性越高。
     • 互信息: 互信息越大则表明两个变量相关性越高，互信息为 0 时，两个变量相互独立。因此可以根据特征变量和目标变量之间的互信息来选择互信息大的特征。
   • 基于模型选择
     • 基于模型参数 / 基于惩罚项的特征选择法 / Embedded / 集成法 : 先使用某些机器学习的算法和模型进行训练，得到各个特征的权值系数，根据系数从大到小选择特征。类似于Filter方法，但是是通过训练来确定特征的优劣。对于线性模型，可以直接基于模型系数大小来决定特征的重要程度。如果想要得到稀疏特征或者说是对特征进行降维，可以在模型上主动使用正则化技术。使用L1正则，调整正则项的权重，基本可以得到任意维度的稀疏特征。
     • 子集选择 / 递归特征消除法 / Wrapper / 包装法: 根据目标函数（通常是预测效果评分），每次选择若干特征，或者排除若干特征。常见的有前向搜索和反向搜索两种思路。如果我们先从N个特征中选出一个最好的特征，然后让其余的N-1个特征分别与第一次选出的特征进行组合，从N-1个二元特征组合中选出最优组合，然后在上次的基础上，添加另一个新的特征，考虑3个特征的组合，依次类推，这种方法叫做前向搜索。反之，如果我们的目标是每次从已有特征中去掉一个特征，并从这些组合中选出最优组合，这种方法就是反向搜索。如果特征数量较多、模型复杂，那么这种选择的过程是非常耗时间和资源的。
     • 基于树模型的特征选择法
   • 降维: 当特征选择完成后，可以直接训练模型了，但是可能由于特征矩阵过大，导致计算量大，训练时间长的问题，因此降低特征矩阵维度也是必不可少的。常见的降维方法有主成分分析法（PCA）和线性判别分析（LDA），线性判别分析本身也是一个分类模型。PCA和LDA有很多的相似点，其本质是要将原始的样本映射到维度更低的样本空间中，但是PCA和LDA的映射目标不一样：PCA是为了让映射后的样本具有最大的发散性；而LDA是为了让映射后的样本有最好的分类性能。所以说PCA是一种无监督的降维方法，而LDA是一种有监督的降维方法。

4. 特征评估

   • 谓特征评估是在将特征灌入模型进行训练之前，事先评估特征的价值，提前发现可能存在的问题，及时解决，避免将有问题的特征导入模型，导致训练过程冗长而得不到好的结果。特征评估是对选择好的特征进行整体评价，而不是特征选择中所谓的对单个特征重要性的评判。特征评估包括特征的覆盖率、特征的维度、定性分析和定量分析等几种方式。
   • 特征的覆盖率是指有多少比例的样本可以构建出相关特征，对于推荐系统来说，存在用户冷启动，因此对于新用户，如果选择的特征中包含从用户行为中获得的特征，那么我们是无法为他构建特征的，从而无法利用模型来为他进行推荐。
   • 特征的维度衡量的是模型的表达能力，维度越高，模型表达能力越强，这时就需要更多的样本量和更多的计算资源、优秀的分布式计算框架来支撑模型的训练。为了达到较好的训练效果，一般对于简单模型可以用更多维度的特征，而对于复杂模型可以用更少的维度。
   • 定性分析是指构建的特征是否跟用户行为是冲突的，可以拿熟悉的样本来做验证，比如在视频推荐中，可以根据自己的行为来定性验证标签的正确性。我个人最喜欢看恐怖电影，那么基于标签构建特征的话，那么对于我的样本，在恐怖这个标签上的权重应该是比其他标签权重大的。
   • 定量分析，通过常用的离线评估指标，如Precitson、Recall、AUC等等来验证模型的效果，当然，最终需要上线做AB测试来看是否对核心用户体验、商业化指标有提升。

Something about FE

Practice

import os
import shutil
import numpy as np
import pandas as pd
import pandas_profiling as pdpf
import time

import warnings
warnings.filterwarnings('ignore')

import matplotlib
import matplotlib.pyplot as plt
import seaborn as sbn
%matplotlib inline

import missingno as msno
import pivottablejs

import lightgbm as lgb
import xgboost as xgb

from sklearn.decomposition import PCA, FastICA, FactorAnalysis, SparsePCA

from sklearn.model_selection import GridSearchCV, cross_val_score, StratifiedKFold, train_test_split
from sklearn.metrics import mean_squared_error, mean_absolute_error

os.chdir(r"D:\Tianchi")

''' 数据含义
SaleID 	交易ID，唯一编码
name 	汽车交易名称，已脱敏
regDate 	汽车注册日期，例如20160101，2016年01月01日
model 	车型编码，已脱敏
brand 	汽车品牌，已脱敏
bodyType 	车身类型：豪华轿车：0，微型车：1，厢型车：2，大巴车：3，敞篷车：4，双门汽车：5，商务车：6，搅拌车：7
fuelType 	燃油类型：汽油：0，柴油：1，液化石油气：2，天然气：3，混合动力：4，其他：5，电动：6
gearbox 	变速箱：手动：0，自动：1
power 	发动机功率：范围 [ 0, 600 ]
kilometer 	汽车已行驶公里，单位万km
notRepairedDamage 	汽车有尚未修复的损坏：是：0，否：1
regionCode 	地区编码，已脱敏
seller 	销售方：个体：0，非个体：1
offerType 	报价类型：提供：0，请求：1
creatDate 	汽车上线时间，即开始售卖时间
price 	二手车交易价格（预测目标）
v系列特征 	匿名特征，包含v0-14在内15个匿名特征
'''

Feature Engineering

Data Washing

data_train = pd.read_csv(r'data/used_car_train_20200313.csv', encoding='utf-8', sep=' ', )
data_test = pd.read_csv(r'data/used_car_testA_20200313.csv', encoding='utf-8', sep=' ', )

print('-'*20)
print(data_train.shape, '\n', data_train.columns)
print(data_train.describe().iloc[:,0:4])
print('-'*20)
print(data_test.shape, '\n', data_test.columns)
print(data_test.describe().iloc[:,0:4])

--------------------
(150000, 31) 
 Index(['SaleID', 'name', 'regDate', 'model', 'brand', 'bodyType', 'fuelType',
       'gearbox', 'power', 'kilometer', 'notRepairedDamage', 'regionCode',
       'seller', 'offerType', 'creatDate', 'price', 'v_0', 'v_1', 'v_2', 'v_3',
       'v_4', 'v_5', 'v_6', 'v_7', 'v_8', 'v_9', 'v_10', 'v_11', 'v_12',
       'v_13', 'v_14'],
      dtype='object')
              SaleID           name       regDate          model
count  150000.000000  150000.000000  1.500000e+05  149999.000000
mean    74999.500000   68349.172873  2.003417e+07      47.129021
std     43301.414527   61103.875095  5.364988e+04      49.536040
min         0.000000       0.000000  1.991000e+07       0.000000
25%     37499.750000   11156.000000  1.999091e+07      10.000000
50%     74999.500000   51638.000000  2.003091e+07      30.000000
75%    112499.250000  118841.250000  2.007111e+07      66.000000
max    149999.000000  196812.000000  2.015121e+07     247.000000
--------------------
(50000, 30) 
 Index(['SaleID', 'name', 'regDate', 'model', 'brand', 'bodyType', 'fuelType',
       'gearbox', 'power', 'kilometer', 'notRepairedDamage', 'regionCode',
       'seller', 'offerType', 'creatDate', 'v_0', 'v_1', 'v_2', 'v_3', 'v_4',
       'v_5', 'v_6', 'v_7', 'v_8', 'v_9', 'v_10', 'v_11', 'v_12', 'v_13',
       'v_14'],
      dtype='object')
              SaleID           name       regDate         model
count   50000.000000   50000.000000  5.000000e+04  50000.000000
mean   174999.500000   68542.223280  2.003393e+07     46.844520
std     14433.901067   61052.808133  5.368870e+04     49.469548
min    150000.000000       0.000000  1.991000e+07      0.000000
25%    162499.750000   11203.500000  1.999091e+07     10.000000
50%    174999.500000   52248.500000  2.003091e+07     29.000000
75%    187499.250000  118856.500000  2.007110e+07     65.000000
max    199999.000000  196805.000000  2.015121e+07    246.000000

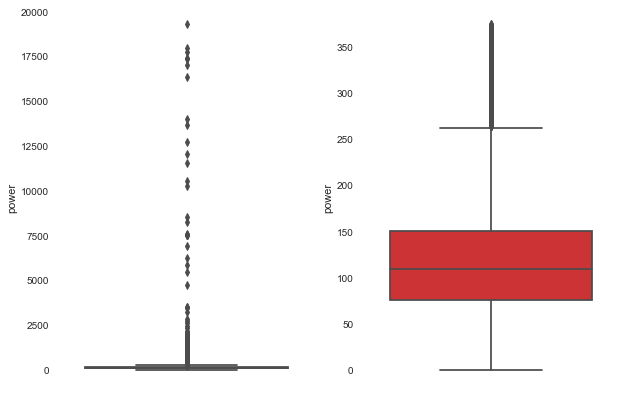
def outliers_proc(data: pd.core.frame.DataFrame, col_name: [str],
                  scale=3) -> pd.core.frame.DataFrame:
    """
    用于清洗异常值，默认用 box_plot（scale=3）进行清洗
    :param data: 接收 dataFrame 数据格式
    :param col_name: pandas 列名
    :param scale: 尺度
    :return:
    """

    def box_plot_outliers(data_ser: pd.core.series.Series,
                          box_scale: int) -> pd.core.series.Series:
        """
        利用箱线图去除异常值
        :param data_ser: 接收 pandas.Series 数据格式
        :param box_scale: 箱线图尺度，
        :return:
        """
        iqr = box_scale * (data_ser.quantile(0.75) - data_ser.quantile(0.25))
        val_low = data_ser.quantile(0.25) - iqr
        val_up = data_ser.quantile(0.75) + iqr
        rule_low = (data_ser < val_low)
        rule_up = (data_ser > val_up)
        return (rule_low, rule_up), (val_low, val_up)

    data_n = data.copy()
    data_series = data_n[col_name]
    rule, value = box_plot_outliers(data_series, box_scale=scale)
    index = np.arange(data_series.shape[0])[rule[0] | rule[1]]
    print("Delete number is: {}".format(len(index)))
    data_n = data_n.drop(index)
    data_n.reset_index(drop=True, inplace=True)
    print("Now column number is: {}".format(data_n.shape[0]))
    index_low = np.arange(data_series.shape[0])[rule[0]]
    outliers = data_series.iloc[index_low]
    print("Description of data less than the lower bound is:")
    print(pd.Series(outliers).describe())
    index_up = np.arange(data_series.shape[0])[rule[1]]
    outliers = data_series.iloc[index_up]
    print("Description of data larger than the upper bound is:")
    print(pd.Series(outliers).describe())

    fig, ax = plt.subplots(1, 2, figsize=(10, 7))
    sbn.boxplot(y=data[col_name], data=data, palette="Set1", ax=ax[0])
    sbn.boxplot(y=data_n[col_name], data=data_n, palette="Set1", ax=ax[1])
    return data_n

data_train = outliers_proc(data_train, 'power', scale=3)

Delete number is: 963
Now column number is: 149037
Description of data less than the lower bound is:
count    0.0
mean     NaN
std      NaN
min      NaN
25%      NaN
50%      NaN
75%      NaN
max      NaN
Name: power, dtype: float64
Description of data larger than the upper bound is:
count      963.000000
mean       846.836968
std       1929.418081
min        376.000000
25%        400.000000
50%        436.000000
75%        514.000000
max      19312.000000
Name: power, dtype: float64

## 训练集和测试集放在一起，方便构造特征
data_train['is_train_data'] = 1
data_test['is_train_data'] = 0
data = pd.concat([data_train, data_test], ignore_index=True)

## 使用时间：data['creatDate'] - data['regDate']，表现汽车使用时间，一般来说价格与使用时间成反比
## 不过要注意，数据里有时间出错的格式，所以我们需要 errors='coerce'
data['used_time'] = (
    pd.to_datetime(data['creatDate'], format='%Y%m%d', errors='coerce') -
    pd.to_datetime(data['regDate'], format='%Y%m%d', errors='coerce')).dt.days

data['city'] = data['regionCode'].apply(lambda x : str(x)[:-3])

## 计算某品牌的销售统计量，同学们还可以计算其他特征的统计量
## 这里要以 train 的数据计算统计量
Train_gb = data_train.groupby("brand")
all_info = {}
for kind, kind_data in Train_gb:
    info = {}
    kind_data = kind_data[kind_data['price'] > 0]
    info['brand_amount'] = len(kind_data)
    info['brand_price_max'] = kind_data.price.max()
    info['brand_price_median'] = kind_data.price.median()
    info['brand_price_min'] = kind_data.price.min()
    info['brand_price_sum'] = kind_data.price.sum()
    info['brand_price_std'] = kind_data.price.std()
    info['brand_price_average'] = round(kind_data.price.sum() / (len(kind_data) + 1), 2)
    all_info[kind] = info
brand_fe = pd.DataFrame(all_info).T.reset_index().rename(columns={"index": "brand"})
data = data.merge(brand_fe, how='left', on='brand')

## 数据分桶 以 power 为例
## 这时候我们的缺失值也进桶了，
## 为什么要做数据分桶呢，原因有很多，= =
## 1. 离散后稀疏向量内积乘法运算速度更快，计算结果也方便存储，容易扩展；
## 2. 离散后的特征对异常值更具鲁棒性，如 age>30 为 1 否则为 0，对于年龄为 200 的也不会对模型造成很大的干扰；
## 3. LR 属于广义线性模型，表达能力有限，经过离散化后，每个变量有单独的权重，这相当于引入了非线性，能够提升模型的表达能力，加大拟合；
## 4. 离散后特征可以进行特征交叉，提升表达能力，由 M+N 个变量编程 M*N 个变量，进一步引入非线形，提升了表达能力；
## 5. 特征离散后模型更稳定，如用户年龄区间，不会因为用户年龄长了一岁就变化

## 当然还有很多原因，LightGBM 在改进 XGBoost 时就增加了数据分桶，增强了模型的泛化性

bin = [i*10 for i in range(31)]
data['power_bin'] = pd.cut(data['power'], bin, labels=False)
data[['power_bin', 'power']].head()

	power_bin	power
0	5.0	60
1	NaN	0
2	16.0	163
3	19.0	193
4	6.0	68

data.drop(['creatDate', 'regDate', 'regionCode'], axis=1, inplace=True)
print(data.shape)
data.columns

(199037, 39)


Index(['SaleID', 'bodyType', 'brand', 'fuelType', 'gearbox', 'is_train_data',
       'kilometer', 'model', 'name', 'notRepairedDamage', 'offerType', 'power',
       'price', 'seller', 'v_0', 'v_1', 'v_10', 'v_11', 'v_12', 'v_13', 'v_14',
       'v_2', 'v_3', 'v_4', 'v_5', 'v_6', 'v_7', 'v_8', 'v_9', 'used_time',
       'city', 'brand_amount', 'brand_price_max', 'brand_price_median',
       'brand_price_min', 'brand_price_sum', 'brand_price_std',
       'brand_price_average', 'power_bin'],
      dtype='object')

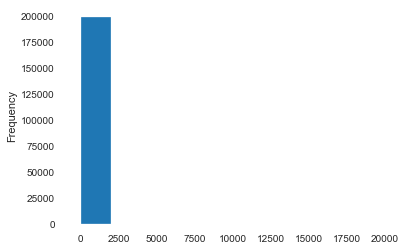
data.to_csv('data_for_tree.csv', index=0)
data['power'].hist()

<matplotlib.axes._subplots.AxesSubplot at 0x267a92468d0>

## 我们对其取 log，再做归一化
from sklearn import preprocessing
min_max_scaler = preprocessing.MinMaxScaler()
data['power'] = np.log(data['power'] + 1) 
data['power'] = ((data['power'] - np.min(data['power'])) / (np.max(data['power']) - np.min(data['power'])))
data['power'].plot.hist()

<matplotlib.axes._subplots.AxesSubplot at 0x267abf56160>

## 所以我们可以直接做归一化
data['kilometer'] = ((data['kilometer'] - np.min(data['kilometer'])) / 
                        (np.max(data['kilometer']) - np.min(data['kilometer'])))
data['kilometer'].plot.hist()

<matplotlib.axes._subplots.AxesSubplot at 0x267adbc2dd8>

def max_min(x):
    return (x - np.min(x)) / (np.max(x) - np.min(x))
data[['brand_amount','brand_price_average','brand_price_max',
'brand_price_median','brand_price_min','brand_price_std',
'brand_price_sum',]] = \
data[['brand_amount','brand_price_average','brand_price_max',
'brand_price_median','brand_price_min','brand_price_std',
'brand_price_sum',]].apply(max_min)

## 对类别特征进行 OneEncoder
data = pd.get_dummies(data, columns=['model', 'brand', 'bodyType', 'fuelType',
                                     'gearbox', 'notRepairedDamage', 'power_bin'])
print(data.shape)
data.columns

(199037, 370)





Index(['SaleID', 'is_train_data', 'kilometer', 'name', 'offerType', 'power',
       'price', 'seller', 'v_0', 'v_1',
       ...
       'power_bin_20.0', 'power_bin_21.0', 'power_bin_22.0', 'power_bin_23.0',
       'power_bin_24.0', 'power_bin_25.0', 'power_bin_26.0', 'power_bin_27.0',
       'power_bin_28.0', 'power_bin_29.0'],
      dtype='object', length=370)

## 这份数据可以给 LR 用
data.to_csv('data_for_lr.csv', index=0)

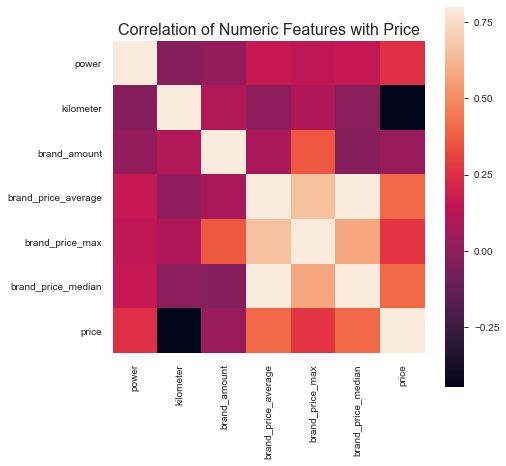
特征-过滤式

## 当然也可以直接看图
data_numeric = data[['power', 'kilometer', 'brand_amount', 'brand_price_average', 
                     'brand_price_max', 'brand_price_median','price']]
correlation = data_numeric.corr()

f , ax = plt.subplots(figsize = (7, 7))
plt.title('Correlation of Numeric Features with Price',y=1,size=16)
sbn.heatmap(correlation,square = True,  vmax=0.8)

<matplotlib.axes._subplots.AxesSubplot at 0x2679cfe6be0>

Modeling and Parameters

Basic Models

1. 线性回归模型：
   • 线性回归对于特征的要求；
   • 处理长尾分布；
   • 理解线性回归模型；
2. 模型性能验证：
   • 评价函数与目标函数；
   • 交叉验证方法；
   • 留一验证方法；
   • 针对时间序列问题的验证；
   • 绘制学习率曲线；
   • 绘制验证曲线；
3. 嵌入式特征选择：
   • Lasso回归；
   • Ridge回归；
   • 决策树；
4. 模型对比：
   • 常用线性模型；
   • 常用非线性模型；
5. 模型调参：
   • 贪心调参方法；
   • 网格调参方法；
   • 贝叶斯调参方法；

Practice

import os
import shutil
import numpy as np
import pandas as pd
import pandas_profiling as pdpf
import time

import warnings
warnings.filterwarnings('ignore')

import matplotlib
import matplotlib.pyplot as plt
import seaborn as sbn
%matplotlib inline

import missingno as msno
import pivottablejs

import lightgbm as lgb
import xgboost as xgb

from sklearn.decomposition import PCA, FastICA, FactorAnalysis, SparsePCA

from sklearn.model_selection import GridSearchCV, cross_val_score, StratifiedKFold, train_test_split
from sklearn.metrics import mean_squared_error, mean_absolute_error

os.chdir(r"D:\Tianchi")

''' 数据含义
SaleID 	交易ID，唯一编码
name 	汽车交易名称，已脱敏
regDate 	汽车注册日期，例如20160101，2016年01月01日
model 	车型编码，已脱敏
brand 	汽车品牌，已脱敏
bodyType 	车身类型：豪华轿车：0，微型车：1，厢型车：2，大巴车：3，敞篷车：4，双门汽车：5，商务车：6，搅拌车：7
fuelType 	燃油类型：汽油：0，柴油：1，液化石油气：2，天然气：3，混合动力：4，其他：5，电动：6
gearbox 	变速箱：手动：0，自动：1
power 	发动机功率：范围 [ 0, 600 ]
kilometer 	汽车已行驶公里，单位万km
notRepairedDamage 	汽车有尚未修复的损坏：是：0，否：1
regionCode 	地区编码，已脱敏
seller 	销售方：个体：0，非个体：1
offerType 	报价类型：提供：0，请求：1
creatDate 	汽车上线时间，即开始售卖时间
price 	二手车交易价格（预测目标）
v系列特征 	匿名特征，包含v0-14在内15个匿名特征
'''

def reduce_mem_usage(df):
    """ iterate through all the columns of a dataframe and modify the data type
        to reduce memory usage.        
    """
    start_mem = df.memory_usage().sum() 
    print('Memory usage of dataframe is {:.2f} MB'.format(start_mem))
    
    for col in df.columns:
        col_type = df[col].dtype
        
        if col_type != object:
            c_min = df[col].min()
            c_max = df[col].max()
            if str(col_type)[:3] == 'int':
                if c_min > np.iinfo(np.int8).min and c_max < np.iinfo(np.int8).max:
                    df[col] = df[col].astype(np.int8)
                elif c_min > np.iinfo(np.int16).min and c_max < np.iinfo(np.int16).max:
                    df[col] = df[col].astype(np.int16)
                elif c_min > np.iinfo(np.int32).min and c_max < np.iinfo(np.int32).max:
                    df[col] = df[col].astype(np.int32)
                elif c_min > np.iinfo(np.int64).min and c_max < np.iinfo(np.int64).max:
                    df[col] = df[col].astype(np.int64)  
            else:
                if c_min > np.finfo(np.float16).min and c_max < np.finfo(np.float16).max:
                    df[col] = df[col].astype(np.float16)
                elif c_min > np.finfo(np.float32).min and c_max < np.finfo(np.float32).max:
                    df[col] = df[col].astype(np.float32)
                else:
                    df[col] = df[col].astype(np.float64)
        else:
            df[col] = df[col].astype('category')

    end_mem = df.memory_usage().sum() 
    print('Memory usage after optimization is: {:.2f} MB'.format(end_mem))
    print('Decreased by {:.1f}%'.format(100 * (start_mem - end_mem) / start_mem))
    return df

sample_feature = reduce_mem_usage(pd.read_csv('data_for_tree.csv'))

Memory usage of dataframe is 62099672.00 MB
Memory usage after optimization is: 16520303.00 MB
Decreased by 73.4%

continuous_feature_names = [x for x in sample_feature.columns if x not in ['price','brand','model','brand']]

sample_feature = sample_feature.dropna().replace('-', 0).reset_index(drop=True)
sample_feature['notRepairedDamage'] = sample_feature['notRepairedDamage'].astype(np.float32)
data_train = sample_feature[continuous_feature_names + ['price']]

data_train_X = data_train[continuous_feature_names]
data_train_y = data_train['price']

from sklearn.linear_model import LinearRegression
model = LinearRegression(normalize=True)
model = model.fit(data_train_X, data_train_y)
'intercept:'+ str(model.intercept_)
sorted(dict(zip(continuous_feature_names, model.coef_)).items(), key=lambda x:x[1], reverse=True)

[('v_6', 3367064.3416418973),
 ('v_8', 700675.5609398854),
 ('v_9', 170630.27723220928),
 ('v_7', 32322.661932026494),
 ('v_12', 20473.67079690079),
 ('v_3', 17868.079541462153),
 ('v_11', 11474.938996675626),
 ('v_13', 11261.764560002604),
 ('v_10', 2683.920090576799),
 ('gearbox', 881.8225039247895),
 ('fuelType', 363.90425072159366),
 ('bodyType', 189.60271012072778),
 ('city', 44.94975120521572),
 ('power', 28.553901616757216),
 ('brand_price_median', 0.5103728134077985),
 ('brand_price_std', 0.4503634709262824),
 ('brand_amount', 0.14881120395066205),
 ('brand_price_max', 0.003191018670313502),
 ('SaleID', 5.3559899198577976e-05),
 ('offerType', 6.017042323946953e-06),
 ('seller', 1.6369158402085304e-06),
 ('is_train_data', -5.66341623198241e-06),
 ('brand_price_sum', -2.1750068681876833e-05),
 ('name', -0.0002980012713063814),
 ('used_time', -0.002515894332869914),
 ('brand_price_average', -0.40490484510104074),
 ('brand_price_min', -2.2467753486894733),
 ('power_bin', -34.42064411731283),
 ('v_14', -274.7841180769423),
 ('kilometer', -372.897526660724),
 ('notRepairedDamage', -495.1903844628292),
 ('v_0', -2045.054957354999),
 ('v_5', -11022.986240536327),
 ('v_4', -15121.731109848046),
 ('v_2', -26098.299920467005),
 ('v_1', -45556.18929728572)]

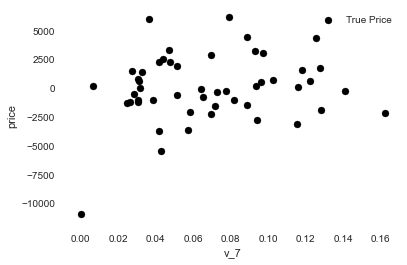
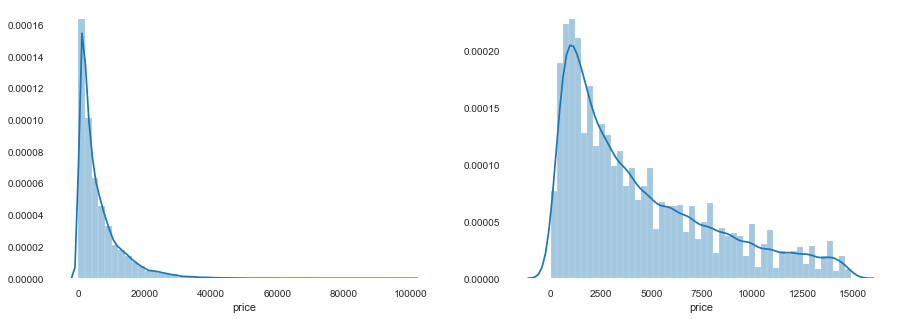
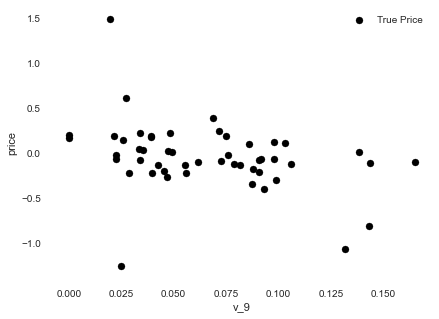
subsample_index = np.random.randint(low=0, high=len(data_train_y), size=50)
plt.scatter(data_train_X['v_9'][subsample_index], 
            data_train_y[subsample_index] - model.predict(data_train_X.loc[subsample_index]), 
            color='black')
## plt.scatter(data_train_X['v_9'][subsample_index], , color='blue')
plt.xlabel('v_7')
plt.ylabel('price')
plt.legend(['True Price','Predicted Price'],loc='upper right')
print('The predicted price is obvious different from true price')
plt.show()

print('It is clear to see the price shows a typical exponential distribution')
plt.figure(figsize=(15,5))
plt.subplot(1,2,1)
sbn.distplot(data_train_y)
plt.subplot(1,2,2)
sbn.distplot(data_train_y[data_train_y < np.quantile(data_train_y, 0.9)])

The predicted price is obvious different from true price

It is clear to see the price shows a typical exponential distribution





<matplotlib.axes._subplots.AxesSubplot at 0x24c80b26f98>

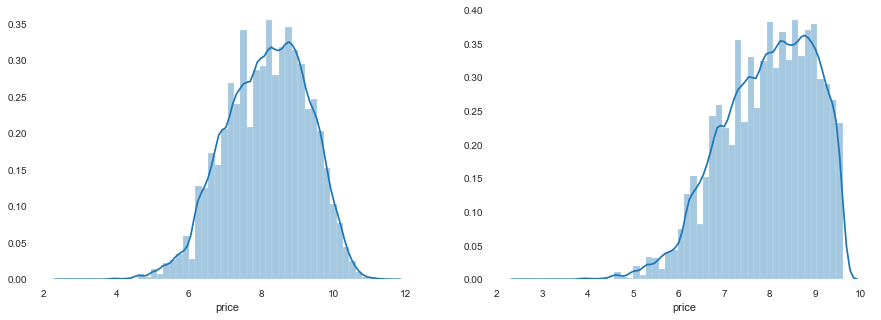
data_train_y_ln = np.log(data_train_y + 1)
print('The transformed price seems like normal distribution')
plt.figure(figsize=(15,5))
plt.subplot(1,2,1)
sbn.distplot(data_train_y_ln)
plt.subplot(1,2,2)
sbn.distplot(data_train_y_ln[data_train_y_ln < np.quantile(data_train_y_ln, 0.9)])

model = model.fit(data_train_X, data_train_y_ln)

print('intercept:'+ str(model.intercept_))
sorted(dict(zip(continuous_feature_names, model.coef_)).items(), key=lambda x:x[1], reverse=True)

subsample_index = np.random.randint(low=0, high=len(data_train_y_ln), size=50)
plt.figure(figsize=(15,5))
plt.subplot(1,2,1)
plt.scatter(data_train_X['v_9'][subsample_index], 
            data_train_y_ln[subsample_index] - model.predict(data_train_X.loc[subsample_index]), 
            color='black')
## plt.scatter(data_train_X['v_9'][subsample_index], , color='blue')
plt.xlabel('v_9')
plt.ylabel('price')
plt.legend(['True Price','Predicted Price'],loc='upper right')

The transformed price seems like normal distribution
intercept:18.750749465662786





<matplotlib.legend.Legend at 0x24c88718e10>

import datetime
sample_feature = sample_feature.reset_index(drop=True)
split_point = len(sample_feature) // 5 * 4

train = sample_feature.loc[:split_point].dropna()
val = sample_feature.loc[split_point:].dropna()

train_X = train[continuous_feature_names]
train_y_ln = np.log(train['price'] + 1)
val_X = val[continuous_feature_names]
val_y_ln = np.log(val['price'] + 1)

model = model.fit(train_X, train_y_ln)
mean_absolute_error(val_y_ln, model.predict(val_X))

0.19577667270300972

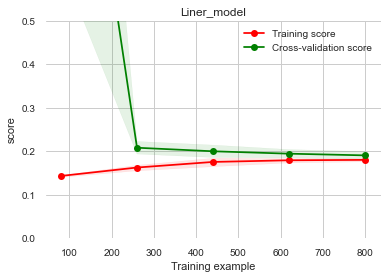
from sklearn.model_selection import learning_curve, validation_curve
from sklearn.model_selection import cross_val_score
from sklearn.metrics import mean_absolute_error,  make_scorer

? learning_curve

def plot_learning_curve(estimator, title, X, y, ylim=None, cv=None, n_jobs=1, train_size=np.linspace(.1, 1.0, 5)):
    plt.figure()
    plt.title(title)
    if ylim is not None:
        plt.ylim(*ylim)
    plt.xlabel('Training example')
    plt.ylabel('score')
    train_sizes, train_scores, test_scores = learning_curve(
        estimator, X, y, cv=cv, n_jobs=n_jobs, train_sizes=train_size, scoring=make_scorer(mean_absolute_error))
    train_scores_mean = np.mean(train_scores, axis=1)
    train_scores_std = np.std(train_scores, axis=1)
    test_scores_mean = np.mean(test_scores, axis=1)
    test_scores_std = np.std(test_scores, axis=1)
    plt.grid()  # 区域
    plt.fill_between(train_sizes, train_scores_mean - train_scores_std,
                     train_scores_mean + train_scores_std, alpha=0.1,
                     color="r")
    plt.fill_between(train_sizes, test_scores_mean - test_scores_std,
                     test_scores_mean + test_scores_std, alpha=0.1,
                     color="g")
    plt.plot(train_sizes, train_scores_mean, 'o-', color='r',
             label="Training score")
    plt.plot(train_sizes, test_scores_mean, 'o-', color="g",
             label="Cross-validation score")
    plt.legend(loc="best")
    return plt


plot_learning_curve(LinearRegression(), 'Liner_model',
                    data_train_X[:1000], data_train_y_ln[:1000], ylim=(0.0, 0.5), cv=5, n_jobs=1)

<module 'matplotlib.pyplot' from 'C:\\Users\\Carlos\\AppData\\Roaming\\Python\\Python36\\site-packages\\matplotlib\\pyplot.py'>

from sklearn.linear_model import LinearRegression, Ridge, Lasso
models = [LinearRegression(), Ridge(), Lasso()]
result = dict()
for model in models:
    model_name = str(model).split('(')[0]
    scores = cross_val_score(model, X=data_train_X, y=data_train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error))
    result[model_name] = scores
    print(model_name + ' is finished')
result = pd.DataFrame(result)
result.index = ['cv' + str(x) for x in range(1, 6)]
result

LinearRegression is finished
Ridge is finished
Lasso is finished

	LinearRegression	Ridge	Lasso
cv1	0.190792	0.194832	0.383899
cv2	0.193758	0.197632	0.381893
cv3	0.194132	0.198123	0.384090
cv4	0.191825	0.195670	0.380526
cv5	0.195758	0.199676	0.383611

from sklearn.linear_model import LinearRegression
from sklearn.svm import SVC
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor
from sklearn.neural_network import MLPRegressor
from xgboost.sklearn import XGBRegressor
from lightgbm.sklearn import LGBMRegressor
models = [LinearRegression(),
          DecisionTreeRegressor(),
          RandomForestRegressor(),
          GradientBoostingRegressor(),
          MLPRegressor(solver='lbfgs', max_iter=100), 
          XGBRegressor(n_estimators = 100, objective='reg:squarederror'), 
          LGBMRegressor(n_estimators = 100)]
result = dict()
for model in models:
    model_name = str(model).split('(')[0]
    scores = cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error))
    result[model_name] = scores
    print(model_name + ' is finished')
result = pd.DataFrame(result)
result.index = ['cv' + str(x) for x in range(1, 6)]
result.T

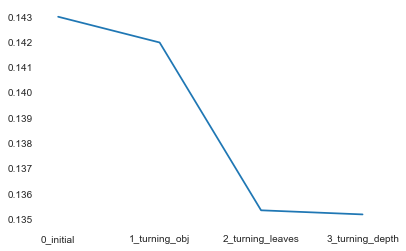
objective = ['regression', 'regression_l1', 'mape', 'huber', 'fair']

num_leaves = [3,5,10,15,20,40, 55]
max_depth = [3,5,10,15,20,40, 55]
bagging_fraction = []
feature_fraction = []
drop_rate = []
best_obj = dict()
for obj in objective:
    model = LGBMRegressor(objective=obj)
    score = np.mean(cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error)))
    best_obj[obj] = score
    
best_leaves = dict()
for leaves in num_leaves:
    model = LGBMRegressor(objective=min(best_obj.items(), key=lambda x:x[1])[0], num_leaves=leaves)
    score = np.mean(cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error)))
    best_leaves[leaves] = score
    
best_depth = dict()
for depth in max_depth:
    model = LGBMRegressor(objective=min(best_obj.items(), key=lambda x:x[1])[0],
                          num_leaves=min(best_leaves.items(), key=lambda x:x[1])[0],
                          max_depth=depth)
    score = np.mean(cross_val_score(model, X=train_X, y=train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error)))
    best_depth[depth] = score
    
sbn.lineplot(x=['0_initial','1_turning_obj','2_turning_leaves','3_turning_depth'], y=[0.143 ,min(best_obj.values()), min(best_leaves.values()), min(best_depth.values())])

<matplotlib.axes._subplots.AxesSubplot at 0x24c92d99438>

from sklearn.model_selection import GridSearchCV
parameters = {'objective': objective , 'num_leaves': num_leaves, 'max_depth': max_depth}
model = LGBMRegressor()
clf = GridSearchCV(model, parameters, cv=5)
clf = clf.fit(data_train_X, data_train_y)
print(clf.best_params_)
model = LGBMRegressor(objective='regression',
                          num_leaves=55,
                          max_depth=15)
np.mean(cross_val_score(model, X=data_train_X, y=data_train_y_ln, verbose=0, cv = 5, scoring=make_scorer(mean_absolute_error)))

{'max_depth': 15, 'num_leaves': 55, 'objective': 'regression'}
0.13754820909576437

Merging

Theory

1

1. 简单加权融合:

   • 回归(分类概率):算术平均融合(Arithmetic mean), 几何平均融合(Geometric mean);
   • 分类:投票(Voting)
   • 综合:排序融合(Rank averaging), log融合

2. stacking/blending:

   • 构建多层模型，并利用预测结果再拟合预测。

3. boosting/bagging(在xgboost, Adaboost, GBDT中已经用到):

   • 多树的提升方法

2

1. 结果层面的融合，这种是最常见的融合方法，其可行的融合方法也有很多，比如根据结果的得分进行加权融合，还可以做Log，exp处理等。在做结果融合的时候，有一个很重要的条件是模型结果的得分要比较近似，然后结果的差异要比较大，这样的结果融合往往有比较好的效果提升。

2. 特征层面的融合，这个层面其实感觉不叫融合，准确说可以叫分割，很多时候如果我们用同种模型训练，可以把特征进行切分给不同的模型，然后在后面进行模型或者结果融合有时也能产生比较好的效果。

3. 模型层面的融合，模型层面的融合可能就涉及模型的堆叠和设计，比如加Staking层，部分模型的结果作为特征输入等，这些就需要多实验和思考了，基于模型层面的融合最好不同模型类型要有一定的差异，用同种模型不同的参数的收益一般是比较小的。

Practice

import os
import shutil
import numpy as np
import pandas as pd
import pandas_profiling as pdpf
import time

import warnings
warnings.filterwarnings('ignore')

import matplotlib
import matplotlib.pyplot as plt
import seaborn as sbn
%matplotlib inline

import missingno as msno
import pivottablejs

import lightgbm as lgb
import xgboost as xgb

from sklearn.decomposition import PCA, FastICA, FactorAnalysis, SparsePCA

from sklearn.model_selection import GridSearchCV, cross_val_score, StratifiedKFold, train_test_split
from sklearn.metrics import mean_squared_error, mean_absolute_error

os.chdir(r"D:\Tianchi")

''' 数据含义
SaleID 	交易ID，唯一编码
name 	汽车交易名称，已脱敏
regDate 	汽车注册日期，例如20160101，2016年01月01日
model 	车型编码，已脱敏
brand 	汽车品牌，已脱敏
bodyType 	车身类型：豪华轿车：0，微型车：1，厢型车：2，大巴车：3，敞篷车：4，双门汽车：5，商务车：6，搅拌车：7
fuelType 	燃油类型：汽油：0，柴油：1，液化石油气：2，天然气：3，混合动力：4，其他：5，电动：6
gearbox 	变速箱：手动：0，自动：1
power 	发动机功率：范围 [ 0, 600 ]
kilometer 	汽车已行驶公里，单位万km
notRepairedDamage 	汽车有尚未修复的损坏：是：0，否：1
regionCode 	地区编码，已脱敏
seller 	销售方：个体：0，非个体：1
offerType 	报价类型：提供：0，请求：1
creatDate 	汽车上线时间，即开始售卖时间
price 	二手车交易价格（预测目标）
v系列特征 	匿名特征，包含v0-14在内15个匿名特征
'''